An Introduction to the Electronic Structure of Atoms
and Molecules
Dr. Richard F.W. Bader
Professor of Chemistry / McMaster University / Hamilton,
Ontario
|
The Quantum Mechanical Explanation of Valency
Helium atoms in their ground state do not form a stable diatomic molecule.
In fact, helium does not combine with any neutral atom. Its valency, that
is, its ability to form chemical bonds with other atoms, is zero. The electronic
configuration of the helium atom is 1s2(¯),
a closed shell configuration.When two helium atoms are in contact, each
electron on one atom encounters an electron on the other atom with a parallel
spin. Because of the Pauli principle, neither electron on either atom can
concentrate its density in the region they have in common, the region between
the nuclei. Instead, the density is transferred to the antibinding regions
behind each nucleus where the overlap of the two atomic density distributions
is least. This is the same effect noted earlier for the approach of two
hydrogen atoms with parallel
spins.
Comparison of a series of density difference maps
for the approach of two helium atoms (Fig. 6-13)
with those given previously for H2 (Fig.
6-10) reveals that one set is the opposite of the other. The regions
of charge build-up and charge depletion are reversed in the two cases.
The density difference diagrams are obtained by subtracting the distribution
obtained by the overlap of the atomic charge densities from the molecular
charge distribution. The former distribution, it will be recalled, does
not place sufficient charge density in the binding region to balance the
force of nuclear repulsion. Thus it is clear from Fig.
6-13 that He2 will be unstable because
the molecular distribution places less charge density in the binding region
than does the one obtained from the overlap of the atomic densities. The
charge density in He2 is transferred to
the antibinding region where it exerts a force which, acting in the same
direction as the nuclear force of repulsion, pulls the two nuclei apart.
Repulsive forces will dominate in He2 and
no stable molecule is possible.
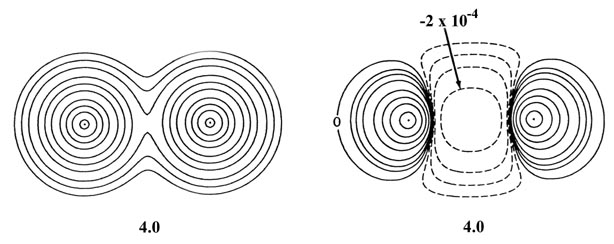
 Fig. 6-13. Contour maps of the total molecular
charge density and of the density difference for two He atoms at internuclear
separations of 4.0 au and 2.0 au. The scale of contour values for the total
density maps are the same as used in Fig 6-9
for H2. The outermost contour is 0.002 au and the innermost
one is 2.0 au for R = 4.0 and R = 2.0 au. The scale used
in the density difference plots is the same as that given in Fig.
6-10 beginning with n = 5 for R = 4.0 au and with
n
= 3 for R = 2.0 au. Note the increase in the amount of charge density
transferred from the binding to the antibinding regions as the separation
between the two atoms is decreased.
Fig. 6-13. Contour maps of the total molecular
charge density and of the density difference for two He atoms at internuclear
separations of 4.0 au and 2.0 au. The scale of contour values for the total
density maps are the same as used in Fig 6-9
for H2. The outermost contour is 0.002 au and the innermost
one is 2.0 au for R = 4.0 and R = 2.0 au. The scale used
in the density difference plots is the same as that given in Fig.
6-10 beginning with n = 5 for R = 4.0 au and with
n
= 3 for R = 2.0 au. Note the increase in the amount of charge density
transferred from the binding to the antibinding regions as the separation
between the two atoms is decreased.
A comparison of the density diiference profiles for He2
(Fig.
6-14) and H2
(Fig.
6-12) provides a striking contrast of the difference between the charge
redistributions which result in the formation of unstable and stable molecules.
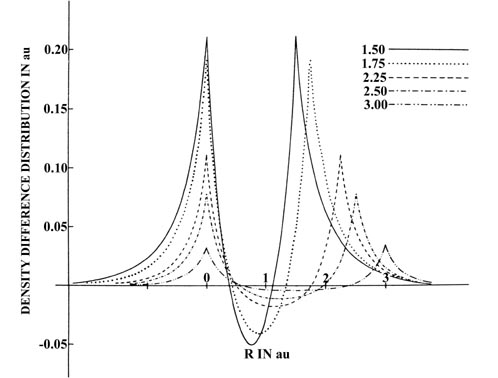
Fig. 6-14. Profiles of the density difference
maps along the internuclear axis for the approach of two He atoms. One
nucleus is held stationary. This figure should be contrasted with Fig.
6-12, the corresponding one for H2.
The force on a helium nucleus in He2
as a function of the internuclear separation is repulsive for the range
of R values indicated in Fig. 6-15.
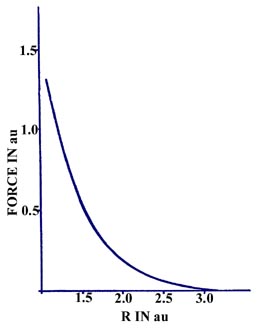 |
Fig. 6-15. Force an a He nucleus in He2
as a function of the internuclear separation. The general form of this
curve is characturistic of an unstabe molecular species. |
Unlike the force curve for H2, there
is no deep minimum in the curve which represents a range of R values
for which the force is attractive. The force curve for He2
does cross the R axis at approximately 6 au (this is not indicated
in Fig. 6-15) and becomes very slightly attractive
for values of R greater than this value. This weak attractive force
has its origin in the long-range mutual polarization of the atomic density
distributions which was discussed in detail for the approach of two hydrogen
atoms. For large internuclear separations, where there is no significant
overlap of the atomic orbitals and hence no need to invoke the Pauli exclusion
principle, the atomic charge distributions of two approaching helium atoms
are polarized in the same way as are the charge distributions for two approaching
hydrogen atoms, and the force is attractive. At smaller internuclear separations,
however, where the overlap of the orbitals is significant and the Pauli
exclusion principle is operative, the direction of the charge transfer
in He2 is reversed and the force is rapidly
transformed into one of repulsion. Were it not for the weak
long-range attractive forces - the van der Waals forces - gaseous
helium could not be condensed into a liquid or a solid phase. As it is,
the force of attraction between two helium atoms is so weak that at a temperature
of only 4.2°K they have sufficient kinetic energy to overcome the forces
of attraction between them and escape into the gas phase.
If it was not necessary to satisfy the demands of the Pauli principle,
electron density would accumulate in the binding region of He2,
even for small values of R, as this region is of lower potential
energy than is the antibinding region. However, when each electron detects
another of like spin (when the orbitals overlap) they cannot concentrate
their charge density in the region they have in common, the binding region.
That it is indeed the Pauli principle which prevents the formation of He2
is evident from the fact that He2+,
which possesses one less electron, is stable! When
a helium atom approaches a helium ion, an orbital vacancy is present and
the density from one pair of electrons (those with opposed spins) can be
concentrated in the binding region.
All the rare gas atoms possess a closed shell structure and this
accounts for their inertness in chemical reactions. No homonuclear diatomic
molecules are found in this group of elements; all occur naturally in the
atomic state. Compounds of Kr and Xe have been formed with fluorine, for
the same reason that the formation of He2+
is possible. Fluorine has a very high electron affinity and a single vacancy
in its outer quantum shell. Thus one of the electrons in the closed shell
structure of Xe can be pulled into the orbital vacancy of the fluorine
atom and density concentrated in the region between the nuclei.
Only an atom with a very high affinity for electrons will
bond with a rare gas atom. The only species found with sufficient electron
affinity to bind a helium atom (which holds its electrons the most tightly
of all atoms) is a He+ ion. If the helium atom has the highest
ionization potential of all the elements, then the singly-charged He+
ion must possess the highest electron affinity of all the neutral or singly-charged
atoms.
Let us now attempt to explain the variation in the valency
exhibited by the elements in the second row of the periodic table. The
hydrides of these elements are LiH, BeH2,
BH3,
CH4, NH3,
OH2 and FH. The valency of the hydrogen
atom is unity as it possesses one unpaired electron and one orbital vacancy.
It can form one electron pair bond. Therefore, the valencies exhibited
in the above hydrides must be 1, 2, 3, 4, 3, 2, 1, as this is the number
of hydrogens bound in each case.
We will consider HF first.
Fluorine. The electron configuration of F is ls22s22p5().
Only one of the electrons in the 2p orbitals is unpaired. The 2p
atomic
orbital with the vacancy may overlap with the 1s atomic orbital
of hydrogen, and if the spin of the electron on H is paired with the spin
of the electron on F, all the requirements for the formation of a stable
chemical bond will be met. The valency of F will be one as it possesses
one unpaired electron and can form one electron pair bond.
Oxygen. The electronic configuration of oxygen is ls22s22p4().
Oxygen has two unpaired electrons, both of which may pair up with an electron
on a hydrogen atom. The valency of oxygen should be two as is observed.
It is obvious that all the requirements for a chemical bond can be met
for every unpaired electron present in the outer or "valency" shell of
an atom. Thus valency may be defined as being equal to the number
of unpaired electrons present in the atom.
Nitrogen. The configuration of nitrogen is ls22s22p3(),
and its hydride should be NH3 as is indeed
the case.
Carbon. Since the most stable electron configuration
of carbon is ls22s22p2()
we predict its valency to be two. The molecule CH2 (called
methylene) is indeed known. However, CH2
is very reactive and its products are not stable until four chemical bonds
are formed to carbon as in the case of CH4.
Four, not two, is the common valency for carbon. How can our theory account
for this fact? The energy of a 2p orbital is not much greater than
that of a 2s orbital. Because of this, relatively little energy
is required to promote an electron from the 2s orbital on carbon
to the vacant 2p orbital:
|
C ls22s22p2()
®
C* ls22s1()2p3()
|
Carbon in the promoted state possesses four unpaired electrons and can
now combine with four hydrogen atoms. Every bond to a hydrogen atom releases
a large amount of energy. The energy required to unpair the 2s electrons
and promote one of them to a 2p orbital is more than compensated
for by the fact that two new CH bonds are obtained.
Boron. Boron has the electronic configuration ls22s22p1().
Its valency should be one and BH is known to exist. However, again through
the mechanism of promotion, the valency of boron can be increased to three:
We might wonder why, with a 2p orbital still vacant, one of the
1s electrons is not promoted and thus give boron a valency of five.
This does not happen because of the large difference in energy between
the 1s and 2p orbitals as shown in the orbital energy level
diagram (Fig. 5-3).
Beryllium. Beryllium has the configuration
ls22s2
and should exhibit a valency of zero. The outer electron configuration
of Be is similar to that of He, a closed shell of s electrons. Indeed,
the molecule Be2 exists only as a weakly
bound van der Waals molecule. However, Be differs from He in that there
are vacant orbitals available in its valency shell. The observed
valency of two in the molecule BeH2 can
be explained by a promotion to the configuration ls22s1()2p1().
Lithium. Lithium, with the configuration ls22s1(),
should exhibit only a valency of one.
Lewis Structures
The concept of an electron pair bond is not restricted to bonds
with hydrogen. The only requirements are an unpaired electron on each atom
(which is another way of saying there is an orbital vacancy on each atom)
with their spins opposed. Thus two fluorine atoms may combine to form the
fluorine molecule F2 through the overlap
of the singly-occupied 2p orbital on one atom with a similar orbital
on the other. This will result in F2 being
described as FF where the single line denotes that one pair of electrons
forms the bond between the two atoms. Similarly, the three singly-occupied
2p orbitals on one nitrogen atom may overlap with those on another
to form the N2 molecule. Since three pairs
of electrons are shared between the nuclei in this case, we represent the
molecule by the symbol NºN.
The electrons in the valence shell of an atom which are not involved in
the formation of a chemical bond (as they are already paired in an orbital
on the atom) may also be indicated and the resulting symbols are called
Lewis
structures. Thus the three pairs of valency electrons on each F,
(2s22p4),
not involved in the bonding are often indicated by dots. For example,
(Lithium has only one outer electron and it is shared in the bond.) In
compounds with nitrogen we may indicate the 2s pair of electrons:
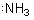 and
and  Recall that each line, since it denoted a bond in these diagrams, represents
a pair of electrons shared between the two atoms joined by the line. If
we add up the lines joined to each atom, multiply by two (to obtain the
number of electrons) and add to this the number of dots which represents
the remaining valence electrons, the number eight is obtained in many cases,
particularly for the second-row elements (n = 2 valence orbitals).
This so-called octet rule results from many elements having four outer
orbitals (nsnpxnpynpz) which together
may contain a total of eight electrons. Not all eight electrons belong
to either atom in general as the electrons in a bond are shared (not necessarily
equally as we shall see) between two atoms. Each bond contains two electrons
with paired spins. Thus the orbital from one atom used to form the bond
is, in a sense, filled as both spin possibilities are now accounted for.
Recall that each line, since it denoted a bond in these diagrams, represents
a pair of electrons shared between the two atoms joined by the line. If
we add up the lines joined to each atom, multiply by two (to obtain the
number of electrons) and add to this the number of dots which represents
the remaining valence electrons, the number eight is obtained in many cases,
particularly for the second-row elements (n = 2 valence orbitals).
This so-called octet rule results from many elements having four outer
orbitals (nsnpxnpynpz) which together
may contain a total of eight electrons. Not all eight electrons belong
to either atom in general as the electrons in a bond are shared (not necessarily
equally as we shall see) between two atoms. Each bond contains two electrons
with paired spins. Thus the orbital from one atom used to form the bond
is, in a sense, filled as both spin possibilities are now accounted for.
The presence of an unshared pair of electrons in the valency
shell of an atom can lead to the formation of another chemical bond. For
example, the unshared pair of electrons in the 2s orbital on nitrogen
in ammonia may attract and bind to the molecule another proton:
H3N:
+ H+ ® NH4+
A similar reaction occurs for the water molecule which possesses two unshared
pairs of electrons:
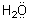 + H+®
+ H+® 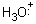 We must modify our previous rule regarding the requirements
for the formation of an electron pair bond. Rather than both orbitals being
half-filled, an orbital on one of the atoms may be filled if the orbital
on the other atom is completely vacant. Molecules possessing an unshared
pair of electrons, which may be used to bond another atom, are called Lewis
bases. Only elements in groups V, VI and VII will exhibit this
property. The elements in groups I to IV do not possess unshared pairs.
Instead, the chemistry of the elements in groups II and III is largely
characterized by the orbital vacancies which they possess in their valency
shell.
We must modify our previous rule regarding the requirements
for the formation of an electron pair bond. Rather than both orbitals being
half-filled, an orbital on one of the atoms may be filled if the orbital
on the other atom is completely vacant. Molecules possessing an unshared
pair of electrons, which may be used to bond another atom, are called Lewis
bases. Only elements in groups V, VI and VII will exhibit this
property. The elements in groups I to IV do not possess unshared pairs.
Instead, the chemistry of the elements in groups II and III is largely
characterized by the orbital vacancies which they possess in their valency
shell.
The compound boron trifluoride represents the pairing of
the three valence electrons of boron with the unpaired electrons on three
F atoms. The boron is considered to be in the promoted configuration ls22s1()2p2()and
BF3is represented as
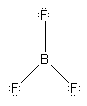
A 2p orbital on boron is vacant. It is not surprising to find
that BF3 may form another bond with a species
which has an unshared pair of electrons, i.e., a Lewis base. For example,
BF3 + : NH3®
H3NBF3
Since BF3 accepts the electron pair it
is termed a Lewis acid. Further examples from group IIIA
are
BF3 + F-
®
BF3-
AlC13 + Cl-®
AlCl4-
BH3+ H-®
BH4-
and from group IIA (which have two orbital vacancies):
BeCl2
+ 2C1- ® BeCl4-2