An Introduction to the Electronic Structure of Atoms and Molecules

While the specific forms of the molecular orbitals (their dependence on r and z in a cylindrical coordinate system) are different for each molecule, their dependence on the angle f as denoted by the quantum number l and their g or u behaviour with respect to inversion are completely determined by the symmetry of the system. These properties are common to all of the molecular orbitals for homonuclear diatomic molecules. In addition, the relative ordering of the orbital energies is the same for nearly all of the homonuclear diatomic molecules. Thus we may construct a molecular orbital energy level diagram, similar to the one used to build up the electronic configurations of the atoms in the periodic table. The molecular orbital energy level diagram (Fig. 8-4) is as fundamental to the understanding of the electronic structure of diatomic molecules as the corresponding atomic orbital diagram is to the understanding of atoms.

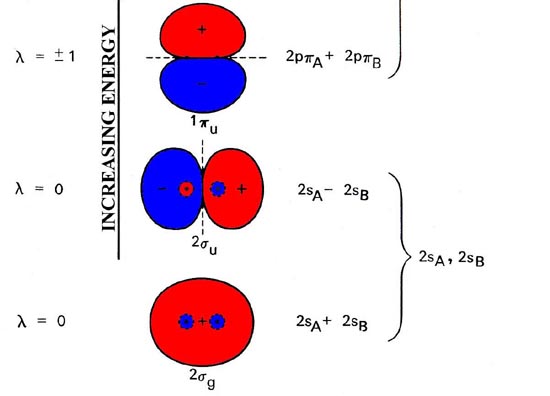
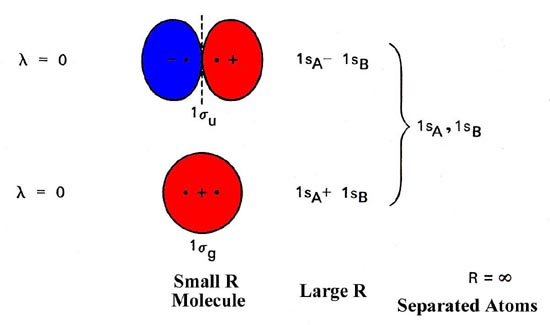
Fig. 8-4.  Molecular orbital energy level diagram for homonuclear diatomic molecules showing the correlation of the molecular orbitals with the atomic orbitals of the separated atoms. The schematic representation of the molecular orbitals is to illustrate their general forms and nodal properties (the nodes are indicated by dashed lines). Only one component of the degenerate 1p_u and 1p_g orbitals is shown. The second component is identical in form in each case but rotated 90° out of the plane. The ordering of the orbital energy levels shown in the figure holds generally for all homonuclear diatomic molecules with the exception of the levels for the 1p_u and 3s_g orbitals, whose relative order is reversed for the molecules after C₂.

   Molecular orbitals exhibit the same general properties as atomic orbitals, including a nodal structure. The nodal properties of the orbitals are indicated in Fig. 8-4. Notice that the nodal properties correctly reflect the g and u character of the orbitals. Inversion of a g orbital interchanges regions of like sign and the orbital is left unchanged. Inversion of a u orbital interchanges the positive regions with the negative regions and the orbital is changed in sign.

   An orbital of a particular symmetry may appear more than once. When this occurs a number is added as a prefix to the symbol. Thus there are 1s_g, 2s_g, 3s_g, etc. molecular orbitals just as there are 1s, 2s, 3s, etc. atomic orbitals. The numerical prefix is similar to the principal quantum number n in the atomic case. As n increases through a given symmetry set, for example, 1s_g, 2s_g, 3s_g, the orbital energy increases, the orbital increases in size and consequently concentrates charge density further from the nuclei, and finally the number of nodes increases as n increases. All these properties are common to atomic orbitals as well.

   We may obtain a qualitative understanding of the molecular orbital energy level diagram by considering the behaviour of the orbitals under certain limiting conditions. The molecular orbital must describe the motion of the electron for all values of the internuclear separation; from R = ¥ for the separated atoms, through R = R_e, the equilibrium state of the molecule, to R = 0, the united atom obtained when the two nuclei in the molecule coalesce (in a hypothetical reaction) to give a single nucleus. Hence a molecular orbital must undergo a continuous change in form. At the limit of large R it must reduce to some combination of atomic orbitals giving the proper orbital description of the separated atoms and for R = 0 it must reduce to a single atomic orbital on the united nucleus.

   Consider, for example, the limiting behaviour of the 1s_g orbital in the case of the hydrogen molecule. The most stable state of H₂ is obtained when both electrons are placed in this orbital with paired spins giving the electronic configuration 1s_g². For large values of the internuclear separation, the hydrogen molecule dissociates into two hydrogen atoms. Thus the limiting form of the 1s_g molecular orbital for an infinite separation between the nuclei should be a sum of 1s orbitals, one centred on each of the nuclei. If we label the two nuclei as A and B we can express the limiting form of the 1s_g orbital as
 

where ls_A is a 1s orbital centred on nucleus A, and ls_B is a ls orbital centred on nucleus B. This form for the 1s_g orbital predicts the correct density distribution for the system at large values of R. Squaring the function (ls_A + ls_B) we obtain for the density
 

  The first two terms denote that one electron is on atom A and one on atom  B, both with 1s atomic density distributions. The cross term 2 ´ ls_A ´ ls_B obtained in the product is zero since the distance between the two nuclei is so great that the overlap of the orbitals vanishes. Notice as well that the function (ls_A + ls_B) has the same symmetry properties as does the 1s_g molecular orbital; it is symmetric with respect to both a rotation about the line joining the nuclei and to an inversion of the coordinates at the mid-point between the nuclei. The 1s_g orbital for the molecule is said to correlate with the sum of 1s orbitals, one on each nucleus, for the separated atom case.

    Consider next the limiting case of the separated atoms for the helium molecule. Of the four electrons present in He₂ two are placed in the 1s_g orbital and the remaining two must, by the Pauli exclusion principle, be placed in the next vacant orbital of lowest energy, the1s_u orbital. The electronic configuration of He₂ is thus 1s_g²1s_u². The  1s_g orbital will correlate with the sum of the 1s  orbitals for the separated helium atoms. Of  the two electrons in the1s_g molecular orbital one will correlate with the 1s orbital on atom A and the other with the 1s orbital on atom B. Since each  helium atom possesses two 1s electrons, the 1s_u orbital must also correlate its electrons with 1s atomic functions on A and B. In addition, the correlated function in this case must be of u symmetry. A function with these properties is
 

The limiting density distribution obtained by squaring this function places one electron in a 1s atomic distribution on A, the other in a 1s atomic distribution on B. The sum of the limiting charge densities for the 1s_g and 1s_u molecular orbitals places two electrons in 1s atomic charge distributions on each atom, the proper description of two isolated helium atoms.

   Every diatomic homonuclear molecular orbital may be correlated with either the sum (for s_g and p_u orbitals) or the difference (for s_u and p_g orbitals) of like orbitals on both separated atoms. By carrying out this correlation procedure for every orbital we may construct a molecular orbital correlation diagram (Fig. 8-4) which relates each of the orbital energy levels in the molecule with the correlated energy levels in the separated atoms. It is important to note that the symmetry of each orbital is preserved in the construction of this diagram. Consider, for example the molecular orbitals which correlate with the 2p atomic orbitals. The direction of approach of the two atoms defines a new axis of quantization for the atomic orbitals. The 2p orbital which lies along this axis is of s symmetry while the remaining two 2p orbitals form a degenerate set of p symmetry with respect to this axis. The sum and difference of the 2ps orbitals on each centre correlate with the 3s_g and 3s_u orbitals respectively, while the sum and the difference of the 2pp orbitals correlate with the p_u and p_g orbitals (Fig. 8-5).

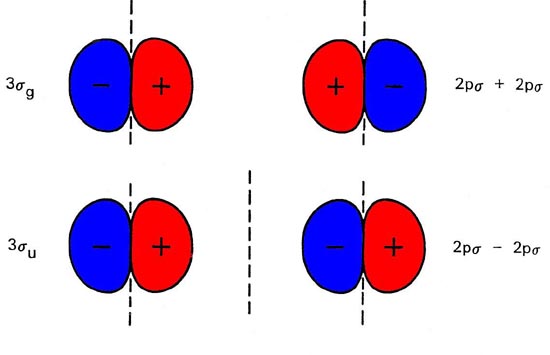
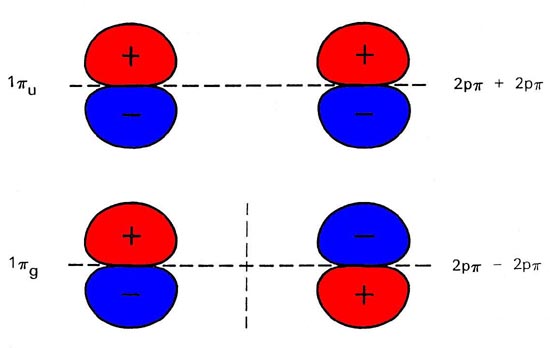
Fig. 8-5.  The correlated separated atom forms of the 3s_g, 3s_u, 1p_u and 1p_g molecular orbitals. The nodal planes are indicated by dashed lines. Only one component of each p orbital is shown.

   For large values of the internuclear distance, each molecular orbital is thus represented by a sum or a difference of atomic orbitals centred on the two interacting atoms. As the atoms approach one another the orbitals on each atom are distorted by polarization and overlap effects. In general, the limiting correlated forms of the molecular orbitals are not suitable descriptions of the molecular orbitals for finite internuclear separations.

   The correlation of the molecular orbitals with the appropriate atomic orbitals of the united atom is left as a problem for the reader (Problem 2).

   We are now in a position to build up and determine the electronic configurations of the homonuclear diatomic molecules by adding electrons two at a time to the molecular orbitals with the spins of the electrons paired, always filling the orbitals of lowest energy first. We shall, at the same time, discuss the effectiveness of each orbital in binding the nuclei and make qualitative predictions regarding the stability of each molecular configuration.

Hydrogen.  The two electrons in the hydrogen molecule may both be accommodated in the 1s_g orbital if their spins are paired and the molecular orbital configuration for H₂  is 1s_g². Since the 1s_g orbital is the only occupied orbital in the ground state of H₂, the density distribution shown previously in Fig. 6-2 for H₂ is also the density distribution for the 1s_g orbital when occupied by two electrons. The remarks made previously regarding the binding of the nuclei in H₂ by the molecular charge distribution apply directly to the properties of the 1s_g charge density. Because it concentrates charge in the binding region and exerts an attractive force on the nuclei the 1s_g orbital is classified as a bonding orbital.

   Excited electronic configurations for molecules may be described and predicted with the same ease within the framework of molecular orbital theory as are the excited configurations of atoms in the corresponding atomic orbital theory. For example, an electron in H₂  may be excited to any of the vacant orbitals of higher energy indicated in the energy level diagram. The excited molecule may return to its ground configuration with the emission of a photon. The energy of the photon will be given approximately by the difference in the energies of the excited orbital and the 1s_g ground state orbital. Thus molecules as well as atoms will exhibit a line spectrum. The electronic line spectrum obtained from a molecule is, however, complicated by the appearance of many accompanying side bands. These have their origin in changes in the vibrational energy of the molecule which accompany the change in electronic energy.

Helium.  The electronic configuration of He₂  is  1s_g² 1s_u². A s_u orbital, unlike a s_g orbital, possesses a node in the plane midway between the nuclei and perpendicular to the bond axis. The 1s_u orbital and all s_u orbitals in general, because of this nodal property, cannot concentrate charge density in the binding region. It is instead concentrated in the antibinding region behind each nucleus (Fig. 8-6).

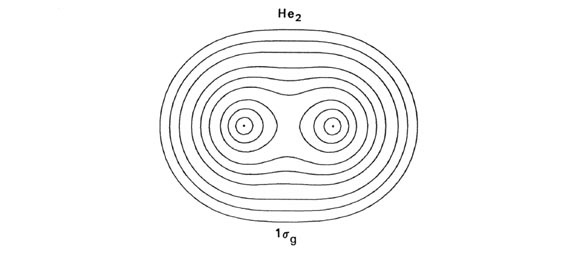
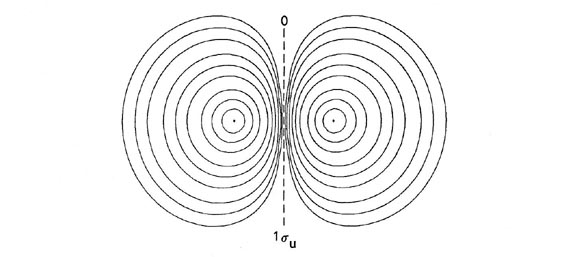
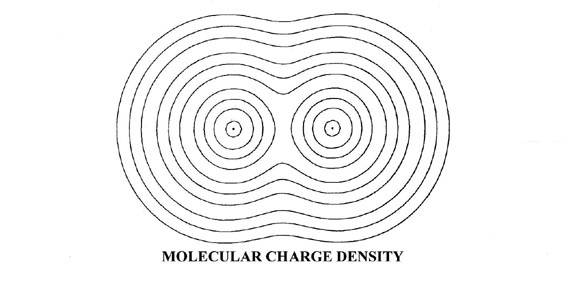
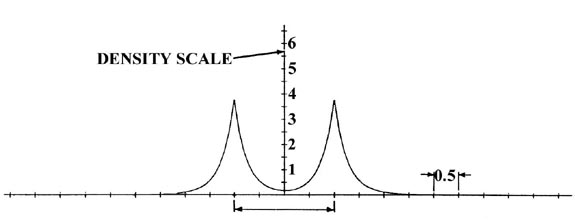
Fig. 8-6.  Contour maps of the doubly-occupied 1s_g and 1s_u molecular orbital charge densities and of the total molecular charge distribution of He₂ at R = 2.0 au. A profile of the total charge distribution along the internuclear axis is also shown. Click here for contour values.

The s_u orbitals are therefore classified as antibonding. It is evident from the form of density distribution for the 1s_u orbital that the charge density in this orbital pulls the nuclei apart rather than drawing them together. Generally, the occupation of an equal number of s_g and s_u orbitals results in an unstable molecule. The attractive force exerted on the nuclei by the charge density in the s_g orbitals is not sufficient to balance both the nuclear force of repulsion and the antibinding force exerted by the density in the s_u orbitals. Thus molecular orbital theory ascribes the instability of He₂ to the equal occupation of bonding and antibonding orbitals. Notice that the Pauli exclusion principle is still the basic cause of the instability. If it were not for the Pauli principle, all four electrons could occupy a s_g-type orbital and concentrate their charge density in the region of low potential energy between the nuclei. It is the Pauli principle, and not a question of energetics, which forces the occupation of the 1s_u antibonding orbital.

   The total molecular charge distribution is obtained by summing the individual molecular orbital densities for single or double occupation numbers as determined by the electronic configuration of the molecule. Thus the total charge distribution for He₂ (Fig. 8-6) is given by the sum of the 1s_g and 1s_u orbital densities for double occupation of both orbitals. The adverse effect which the nodal property of the 1s_u orbital has on the stability of He₂ is very evident in the total charge distribution. Very little charge density is accumulated in the central portion of the binding region. The value of the charge density at the mid-point of the bond in He₂ is only 0.164 au compared to a value of 0.268 au for H₂.

   We should reconsider in the light of molecular orbital theory the stability of He₂⁺ and the instability of the hydrogen molecule with parallel spins, cases discussed previously in terms of valence bond theory. He₂⁺ will have the configuration 1s_g² 1s_u¹. Since the 1s_u orbital is only singly occupied in He₂⁺, less charge density is accumulated in the antibinding regions than is accumulated in these same regions in the neutral molecule. Thus the binding forces of the doubly-occupied 1s_g density predominate and He₂ is stable. The electron configuration of H₂ is 1s_g¹(­)1s_u¹(­) when the electronic spins are parallel. The electrons must occupy separate orbitals because of the Pauli exclusion principle. With equal occupation of bonding and antibonding orbitals, the H₂ (­­)species is predicted to be unstable.

Lithium.  The Li₂ molecule with the configuration 1s_g²1s_u²2s_g² marks the beginning of what can be called the second quantum shell in analogy with the atomic case. Since the 1s_u antibonding orbital approximately cancels the binding obtained from the 1s_g bonding orbital, the bonding in Li₂ can be described as arising from the single pair of electrons in the 2s_g orbital. Valence bond theory, or a Lewis model for Li₂, also describes the bonding in Li₂ as resulting from a single electron pair bond. This is a general result. The number of bonds predicted in a simple Lewis structure is often found to equal the difference between the number of occupied bonding and antibonding orbitals of molecular orbital theory.

   The forms of the orbital density distributions for Li₂ (Fig. 8-7) bear out the prediction that a single electron pair bond is responsible for the binding in this molecule.

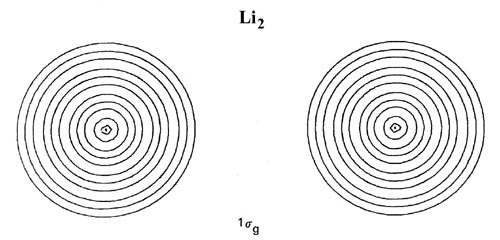
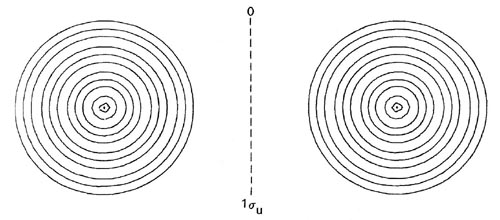
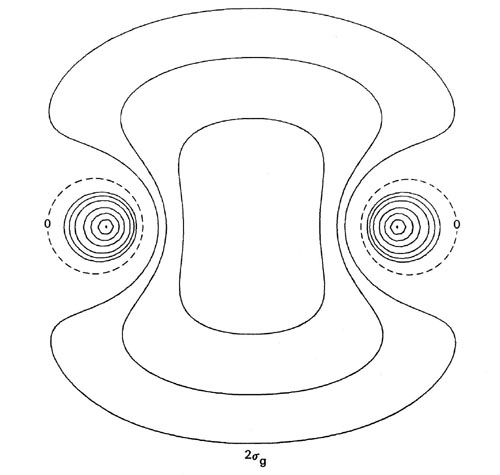
Fig. 8-7.  Contour maps of the doubly-occupied 1s_g, 1s_u and 2s_g  molecular orbital charge densities for Li₂ at R = 5.051 au, the equilibrium internuclear separation. Click here for contour values. The total molecular charge distribution for Li₂ is shown in Fig. 7-3.

The 1s_g and 1s_u density distributions are both strongly localized in the regions of the nuclei with spherical contours characteristic of 1s atomic distributions. The addition of just the doubly-occupied 1s_g and 1s_u orbital densities in Li₂ will yield a distribution which resembles very closely and may be identified with the doubly-occupied 1s or inner shell atomic densities on each lithium nucleus. Only the charge density of the pair of valence electrons in the 2s_g orbital is delocalized over the whole of the molecule and accumulated to any extent in the binding region.

   Thus there are cases where the molecular orbitals even at the equilibrium bond length resemble closely their limiting atomic forms. This occurs for inner shell molecular orbitals which correlate with the inner shell atomic orbitals on the separated atoms. Inner shell 1s electrons are bound very tightly to the nucleus as they experience almost the full nuclear charge and the effective radii of the 1s density distributions are less than the molecular bond lengths. Because of their tight binding and restricted extension in space, the inner electrons do not participate to any large extent in the binding of a molecule. Thus with the exception of H₂ and He₂ and their molecular ions, the 1s_g and 1s_u molecular orbitals degenerate into non-overlapping atomic-like orbitals centred on the two nuclei and are classed as nonbonding orbitals.

Beryllium.  The configuration of Be₂ is 1s_g²1s_u²2s_g²2s_u² and the molecule is predicted to form a weakly bound van der Waals moecule.

Oxygen.  Since the method of determining electronic configurations is clear from the above examples, we shall consider just one more molecule in detail, the oxygen molecule. Filling the orbitals in order of increasing energy the sixteen electrons of O₂ are described by the configuration 1s_g²1s_u²2s_g²2s_u²3s_g²1p_u⁴1p_g². The orbital densities are illustrated in Fig. 8-8.

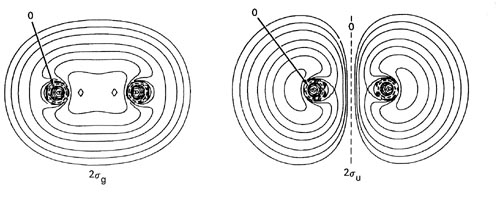
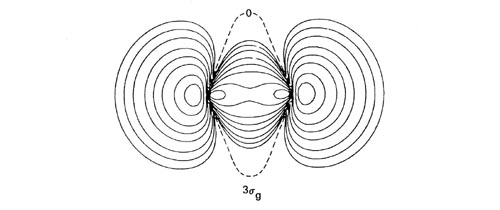
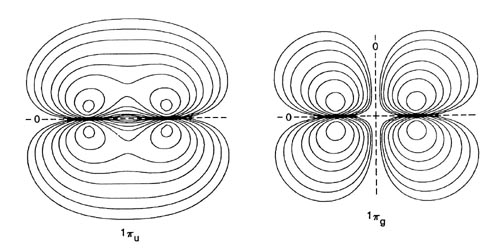
Fig. 8-8.  Contour maps of the molecular orbital charge densities for O₂ at the equilibrium internuclear distance of 2.282 au. Only one component of the Ip_g and 1p_u orbitals is shown. All the maps are for doubly-occupied orbitals with the exception of that for 1p_g for which each component of the doubly-degenerate orbital contains a single electron. The nodes are indicated by dashed lines. Click here for contour values.

   The molecular orbitals of p symmetry are doubly degenerate and a filled set of p orbitals will contain four electrons. The node in a p_u orbital is in the plane which contains the internuclear axis and is not perpendicular to this axis as is the node in a s_u orbital. (The nodal properties of the orbitals are indicated in Fig. 8-4.) The p_u orbital is therefore bonding. A p_g orbital, on the other hand, is antibonding because it has, in addition to the node in the plane of the bond axis, another at the bond mid-point perpendicular to the axis. The bonding and antibonding characters of the p orbitals have just the opposite relationship to their g and u dependence as have the s orbitals.

   The 1s_g and 1s_u orbital densities have, as in the case of Li₂, degenerated into localized atomic distributions with the characteristics of 1s core densities and are nonbonding. The valence electrons of O₂ are contained in the remaining orbitals, a feature reflected in the extent to which their density distributions are delocalized over the entire molecule. Aside from the inner nodes encircling the nuclei, the 2s_g and 2s_uorbital densities resemble the 1s_g and 1s_u valence density distributions of H₂ and He₂. A quantitative discussion of the relative binding abilities of the 2s_g , 3s_g and 1p orbital densities is presented in the following section.

   One interesting feature of the electronic configuration of O₂ is that its outer orbital is not fully occupied. The two p_g electrons could both occupy one of the p_g orbitals with paired spins or they could be assigned one to each of the p_g orbitals and have parallel spins. Hund's principle applies to molecules as well as to atoms and the configuration with single occupation of both p_g orbitals with parallel spins is thus predicted to be the most stable. This prediction of molecular orbital theory regarding the electronic structure of O₂ has an interesting consequence. The oxygen molecule should be magnetic because of the resultant spin angular momentum possessed by the electrons. The magnetism of O₂ can be demonstrated experimentally in many ways, one of the simplest being the observation that liquid oxygen is attracted to the poles of a strong magnet.