An Introduction to the Electronic Structure of Atoms
and Molecules
Dr. Richard F.W. Bader
Professor of Chemistry / McMaster University / Hamilton,
Ontario
|
The Effect of the Pauli Principle on Chemical Binding
The Pauli exclusion principle plays as important a role in the understanding
of the electronic structure of molecules as it does in the case of atoms.
The end result of the Pauli principle is to limit the amount of electronic
charge density that can be placed at any one point in space. For example,
the Pauli principle prevents the 1s orbital in an atom from containing
more than two electrons. Since the 1s orbital places most of its
charge density in regions close to the nucleus, the Pauli principle, by
limiting the occupation of the 1s orbital, limits the amount of
density close to the nucleus. Any remaining electrons must be placed in
orbitals which concentrate their charge density further from the nucleus.
In an earlier discussion we pointed out that the reason
the electron doesn't fall onto the nucleus is because it must possess kinetic
energy if Heisenberg's uncertainty principle is not to be violated. This
is one reason why matter doesn't collapse. The Pauli principle is equally
important in this regard. The electron density of the outer electrons in
an atom cannot collapse and move closer to the nucleus since it can do
so only if the electrons occupy an orbital with a lower n value.
If, however, the inner orbital contains two electrons, then the Pauli principle
states that the collapse cannot occur. We must be careful in our interpretation
of this aspect of the Pauli principle. The density from a 2s orbital
has a small but finite probability of being found well within the density
of the 1s orbital. Do not interpret the Pauli principle as
implying that the density from an occupied orbital has a clearly defined
and distinct region in real space all to its own. This is not the
case. The operation of the Pauli principle is more subtle than this. In
some simple cases, such as the ones we wish to discuss below, the limiting
effect of the Pauli principle on the density distribution can, however,
be calculated and pictured in a very direct manner.
The Pauli principle demands that when two electrons are
placed in the same orbital their spins must be paired. What restriction
is placed on the spins of the electrons during the formation of a molecule,
when two orbitals, each on a different atom, overlap one another? For example,
consider the approach of two hydrogen atoms to form a hydrogen molecule.
Consider atom A to have the configuration 1s1()and
atom B the configuration 1s1(¯).
Even when the atoms approach very close to one another the Pauli principle
would be satisfied as the spins of the two electrons are opposed. This
is the situation we have tacitly assumed in our previous discussion of
the hydrogen molecule. However, what would occur if two hydrogen atoms
approached one another and both had the same configuration and spin, say
1s1()?
When two atoms are relatively close together the electrons become indistinguishable.
It is no longer possible to say which electron is associated with which
atom as both electrons move in the vicinity of both nuclei. Indeed this
is the effect which gives rise to the chemical bond. In so far as we can
still regard the region around each atom to be governed by its own atomic
orbital, distorted as it may be, two electrons with the same spin will
not be able to concentrate their density in the binding region. This region
is common to the orbitals on both atoms, and since the electrons possess
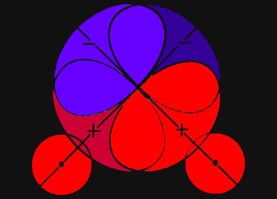
the same spin they cannot both be there simultaneously. In the region of
greatest overlap of the orbitals, the binding region, the presence of one
electron will tend to exclude the presence of the other if their spins
are parallel. Instead of density accumulating in the binding region as
two atoms approach, electron density is removed from this region and placed
in the antibinding region behind each nucleus where the overlap of the
orbitals is much smaller. Thus the approach of two hydrogen atoms with
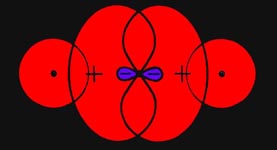
parallel spins does not result in the formation of a stable molecule. This
repulsive state of the hydrogen molecule, in which both electrons have
the same spin and atomic orbital quantum numbers, can be detected spectroscopically.
We can now give the general requirements for the
formation of a chemical bond. Electron density must be accumulated in the
region between the nuclei to an extent greater than that obtained by allowing
the original atomic density distributions to overlap. In general, the increase
in charge density necessary to balance the nuclear force of repulsion requires
the presence of two electrons. (Click
here for note.)
In the atomic orbital approximation we picture the bond as resulting
from the overlap of two distorted atomic orbitals, one centred on each
nucleus. When the orbitals overlap, both electrons may move in the field
of either nuclear charge as the electrons may now exchange orbitals. Finally,
the pair of electrons must possess opposed spins. When their spins are
parallel, the charge density from each electron is accumulated in the antibinding
rather than in the binding region.
We shall now apply these principles to a number of
examples and in doing so obtain a quantum mechanical definition of valency.