An Introduction to the Electronic Structure of Atoms and Molecules

  Any chemical bond results from the accumulation of charge density in the binding region to an extent sufficient to balance the forces of repulsion. Ionic and covalent binding represent the two possible extremes of reaching this state of electrostatic equilibrium and there is a complete spectrum of bond densities lying between these two extremes. Since covalent and ionic charge distributions exhibit radically different chemical and physical properties, it is important, if we are to understand and predict the bulk properties of matter, to know which of the two extremes of binding a given molecule most closely approximates.

   We can obtain an experimental measure of the extent to which the charge density is unequally shared by the nuclei in a molecule. The physical property which determines the asymmetry of a charge distribution is called the dipole moment. To illustrate the definition of the dipole moment we shall determine this property for the LiF molecule assuming that one electron is transferred from Li to F and that the charge distributions of the resulting ions are spherical.

    The dipole moment is defined as the product of the total amount of positive or negative charge and the distance between their centroids  The centroids of the positive and negative charges in a molecule are determined in a manner similar to that used to determine the centre of mass of a system.

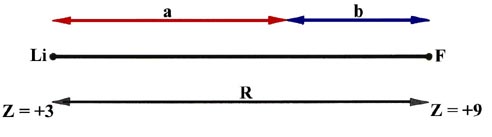
Fig.7-6. diagram for the calculation of the centroids of positive and negative charge in LiF.

With reference to Fig. 7-6 the "centre of gravity" of the positive charge in LiF is easily found from the following equations:
  Eliminating b from these equations and solving for a we find that
  Thus all the positive charge in the LiF molecule can be considered to be at a point one quarter of the bond length away from the fluorine nucleus. Similarly the centroid of negative charge, remembering that one electron has been transferred from Li to F, is found to lie at a point one sixth of the bond length away from the F nucleus. The centroids of positive and negative charge do not coincide, the negative centroid being closer to the F nucleus than the positive centroid. While the molecule is electrically neutral, there is a separation of charge within the molecule. Let us denote the distance between the centroids of charge by l :
  and since there are twelve electrons in LiF, the dipole moment denoted by m is
  Thus, not surprisingly, the dipole moment in this case is numerically equal to one excess positive charge at the Li nucleus and one excess negative charge at the F nucleus, or one pair of opposite charges separated by the bond length.

   We can easily calculate the value of the dipole moment. The value of R for LiF is 1.53 ´ 10^-8 cm and the charge on the electron is 4.80 ´ 10^-10 esu. Thus
 

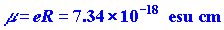
	or

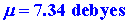where 1 debye = 1 ´ 10^-18 esu cm. (The fundamental unit for dipole moments is called a debye in honour of P. Debye who was responsible for formulating the theory and method of measurement of this important physical quantity.) The experimental value of m for LiF is slightly smaller than the calculated value, being 6.28 debyes. The reason for the discrepancy is easily traced to the assumption made in the calculation that the charge distributions of the Li⁺ and F^- ions are spherical. We have previously indicated that the charge distributions of both the F^- and Li⁺ ions are polarized in a direction counter to the direction of transfer of the electron in order to balance the forces on the nuclei. The centroid of the ten negative charges on F is not at the F nucleus, but shifted slightly towards the Li, and the centroid of the charge density on Li⁺ is correspondingly shifted slightly off  the Li nucleus away from the F. Thus the centroid of negative charge for the whole molecule is not as close to the F nucleus as our simple calculation indicated and the dipole moment is correspondingly less.

   Obviously from this discussion the dipole moment of a molecule with a covalent bond will be zero since the symmetry of the charge distribution will dictate that the positive and negative charge centroids coincide. Thus dipole moments can conceivably possess values which lie between the covalent limit of zero and the ionic extreme which approaches neR in value (n being the number of electrons transferred in the formation of the ionic bond).

   The series of diatomic molecules formed by the union of a single hydrogen atom with each of the elements in the second row of the periodic table exemplifies both the extreme and intermediate types of binding, and hence of dipole moments. Table 7-4 lists the dipole moments and the values of eR for the ionic extreme (assuming spherical ions) for the second-row diatomic hydride molecules.

All of these molecules exist as stable, independent species in the gas phase at low pressures and may be studied by spectroscopic methods or by molecular beam techniques. Only LiH and HF, however, are stable under normal conditions; LiH is a solid and HF a gas at room temperature. The remaining diatomic hydrides are very reactive since they are all capable of forming one or more additional bonds.

   The variation of the dipole moment in this series of molecules provides a measure of the relative abilities of H and of each of the second-row elements to attract electrons. For example, the dipole moment for LiH illustrates that electron density is transferred from Li to H in the formation of this molecule. In HF, on the other hand, charge density is transferred from H to F. With the exception of BH, there is a steady increase in m from -6.0 debyes for LiH to +1.9 debyes for HF. Only LiH approaches the ionic limit of Li⁺H^-. BeH appears to possess a close to equal sharing of the valence electrons. The remaining molecules, while exhibiting some degree of charge removal from H, are all far removed from the ionic extreme. They represent cases of molecular binding which lie between the two extremes, ionic and covalent. They are referred to as polar molecules.

  We can best illustrate the variation in the chemical binding in this series of molecules by considering the properties of the molecular charge and bond density distributions (Fig. 7-7 and 7-8). In LiH almost all of the molecular charge density is centred on the two nuclei in nearly spherical distributions.

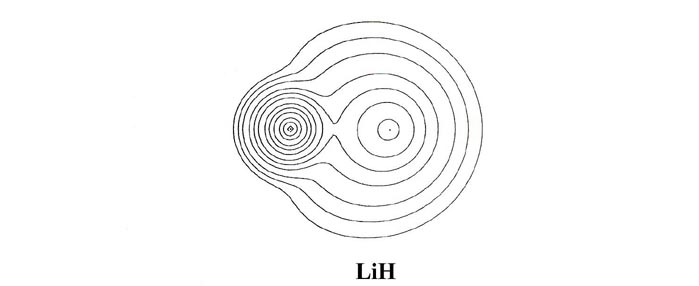
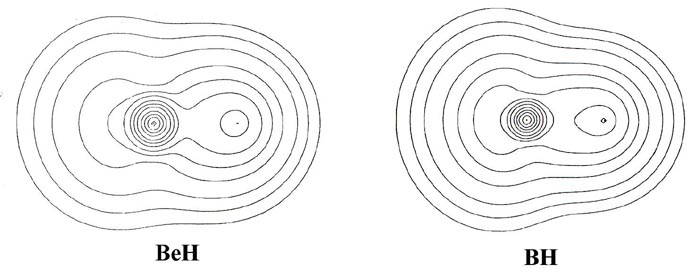
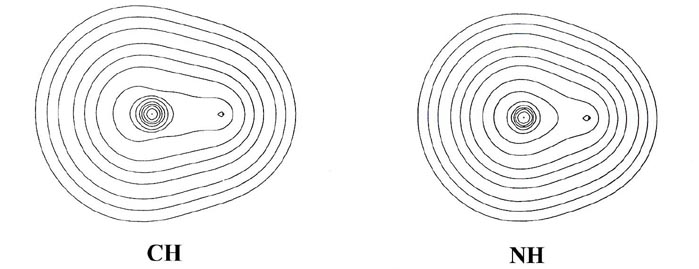
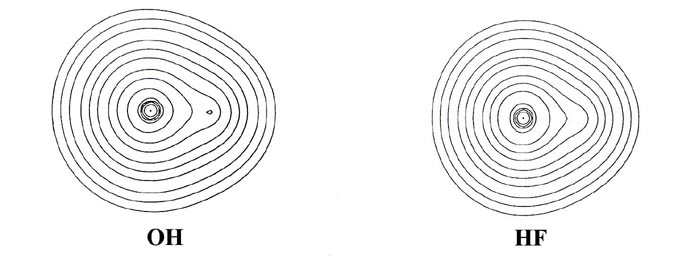
Fig. 7-7. Contour maps of the molecular charge distrubution of the diatomic hydride molecules LiH to HF. The proton is the nucleus on the right-hand side in each case. Click here for contour values.

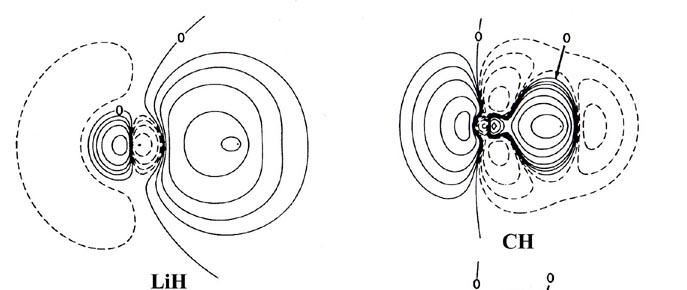
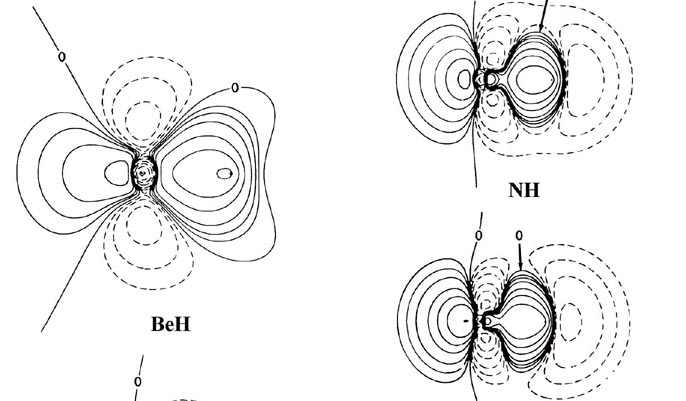
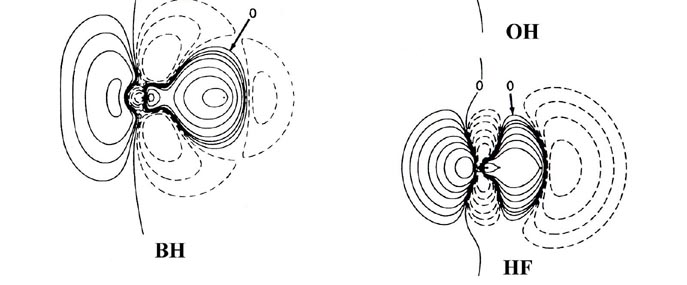
Fig. 7-8. Bond density maps for the diatiomic hydride molecules LiH to HF. The proton is on the right-hand side in each case. Click here for contour values.

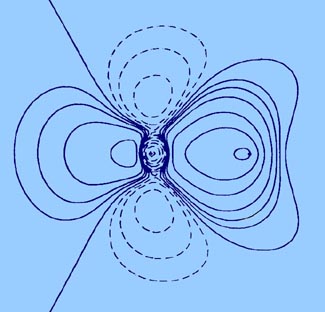
The nonbonded charge and radius for lithium, 1.09 e^- and 1.7 a_o respectively, are characteristic of the 1s² inner shell distribution of Li⁺. Thus the molecular charge distribution for LiH indicates that the single valence electron of lithium is transferred to hydrogen and that the bond is ionic. (Recall that initially the Li atom is much larger than an H atom. The density map for LiH should be compared to that given previously for LiF, Fig. 7-1.)

   In BeH, the valence density has the appearance of being equally shared by the two nuclei. From BH through to HF a decreasing amount of density is centred on the proton to the extent that the charge distribution of HF could be approximately described as an F^- ion distribution polarized by an imbedded proton.

   The increase of the effective nuclear charge across a row of the periodic table is reflected not only in the amount of charge transferred to or from the hydrogen, but also in the relative sizes of the molecules. In BeH the density is diffuse and the molecule is correspondingly large. In HF the density is more compact and the molecule is the smallest in the series. The decrease in the size of the molecule from BH to HF parallels the decrease in the size of the atoms B to F. The intermediate size of LiH is a consequence of the one and only valence electron of lithium being transferred to hydrogen, and thus the size of LiH is a reflection of the size of the Li⁺ ion and not of the Li atom.

    In general terms, the bond density maps provide a striking confirmation of the transfer of charge predicted by the relative electron affinities or by the relative effective nuclear charges of hydrogen and the second-row elements Li ® F. We may again employ the position of the charge increase in the bond density map to characterize the type of binding present in the molecule. The map for LiH exhibits the same characteristics as does the one for LiF (Fig. 7-2), the contours in the region of the Li nucleus being remarkably similar in the two cases. The valence density is clearly localized about the proton just as it is about the fluorine nucleus in LiF. The 1s core density remaining on lithium is clearly polarized away from the proton, and the density increase localized on the proton is polarized towards the lithium as required in ionic binding.

   The one principal difference between the LiH and LiF bond density maps concerns the shape of the contours representing the density increase on the proton and fluorine nucleus. In LiF the contours on fluorine are similar in shape to those obtained for a 2ps orbital density. In LiH the contours on the proton are nearly spherical. In terms of a simple orbital model we imagine the 2s electron of Li to be transferred to the 1s orbital of hydrogen in LiH and to the 2ps orbital of fluorine in LiF. The spherical and double-lobed appearance of the density increases found for hydrogen and fluorine respectively show these orbital models of the binding to be reasonable ones.

   From BeH through the rest of the series, the bond density maps show an increase in the amount of charge removed from the proton and transferred to the region of the other nucleus. This is evident from the increase in the number and diameter of the dashed contours in the nonbonded region of the proton. The pattern of charge increase and charge removal in the regions of the Be, B, C, N, O and F nuclei is similar to that found for these nuclei in their homonuclear diatomic molecules, and is characteristic of the participation of a ps orbital in the formation of the bond. The polarization of the density in the region of the hydrogen is of the simple dipolar type characteristic of a dominant s orbital contribution. As previously discussed, the double-lobed appearance of the density increase in the region of fluorine in the bond density map for LiF can be viewed as characteristic of the ionic case when a 2ps orbital vacancy is filled in forming the bond. This limiting pattern is most closely approached in the hydride series by HF, the molecule exhibiting the largest degree of charge transfer from hydrogen. HF, of all the hydrides, is most likely to approach the limiting ionic extreme of H⁺F^-. However, the charge increase in the region of fluorine in HF is not as symmetrical as that found for F in the LiF molecule. The proton in HF, unlike the Li⁺ ion in LiF, is imbedded in one lobe of the density increase on F and distorts it. Thus, unlike the ionic extreme of LiF, the charge increase on F in HF is shared by both nuclei in the molecule.

   Another important difference between the charge distributions of HF and LiF concerns the polarizations of the charge density in the immediate vicinities of the nuclei. In LiF (or LiH) the localized charge distributions are both polarized in a direction opposite to the direction of charge transfer Li ® F (or Li ® H). These polarizations are a consequence of the extreme charge transfer from lithium to fluorine, a transfer resulting in a force of attraction on the lithium nucleus and one of repulsion on the fluorine nucleus. In HF the charge density in the regions of the proton and the fluorine nucleus is polarized in the same direction as the direction of charge transfer from H ® F. Thus the amount of charge transferred to the vicinity of the fluorine in HF is not, unlike the situation in LiF, sufficient to screen the nuclear charge of fluorine and hence exert a net attractive force on the proton. Instead, the fluorine nucleus and its associated charge density exert a net repulsive force on the proton, one which is balanced by the inwards polarization of the charge density in the region of the proton.

   The polarization of the charge density on the proton adds to and is contiguous with the charge increase in the binding region. Thus in HF and in the molecules BeH to OH for which the charge transfer is less extreme, the nuclei are bound by a shared density increase and the binding is covalent. From BeH through the series of molecules the sharing of the charge increase in the binding region becomes increasingly unequal and favours the heavy nucleus over the proton. The latter molecules in the series, NH, OH and HF, provide examples of polar binding which are intermediate between the extremes of perfect covalent and ionic binding as exhibited by the homo nuclear diatomics and LiF respectively.

   In general, chemical bonds between identical atoms or between atoms from the same family in the periodic table will exhibit equal or close to equal sharing of the bond density and be covalent in character. Compounds formed by the union of elements in columns I or II with elements in columns VIA or VIIA will be ionic, as exemplified by LiF or BeO. We find a continuous change from covalent to ionic binding as the atoms joined by a chemical bond come from columns in the periodic table which are progressively further removed from one another. This is illustrated by the variation in the molecular charge distributions through the series of molecules shown in Fig. 7-9.

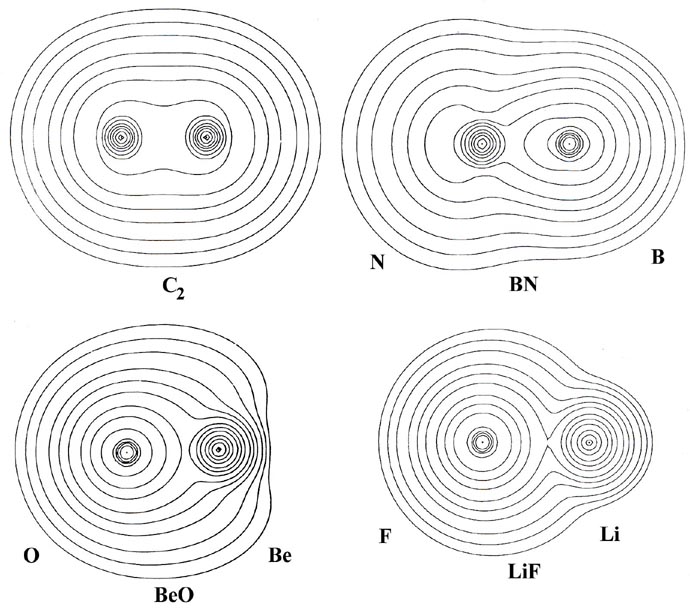
Fig. 7-9.  Molecular charge distributions for the 12-electron isoelectronic series C₂, BN, BeO and LiF. Click here for contour values.

This series of molecules is formed (in an imaginary process) by the successive transfer of one nuclear charge from the nucleus on the left to the nucleus on the right, starting with the central symmetrical molecule C₂.

The molecules are said to form an isoelectronic series since they all contain the same number of electrons, twelve. The molecular charge distributions in this series illustrate how the charge distribution and binding for a constant  number of electrons changes as the nuclear potential field in which the electrons move is made increasingly unsymmetrical.

   In C₂ the nuclear charges are, of course, equal and the charge distribution is symmetrically shared by both nuclei in the manner characteristic of covalent binding. In the remaining molecules the valence charge density is increasingly localized in the region of the left-hand nucleus. This is particularly evident in the bond density maps and their profiles (Fig. 7-10) which show the increasing extent to which charge density is transferred from the region of the nucleus on the right (B, Be, Li) to its partner on the left  (N, 0, F).

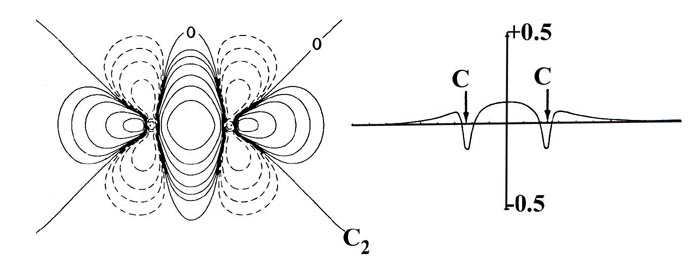
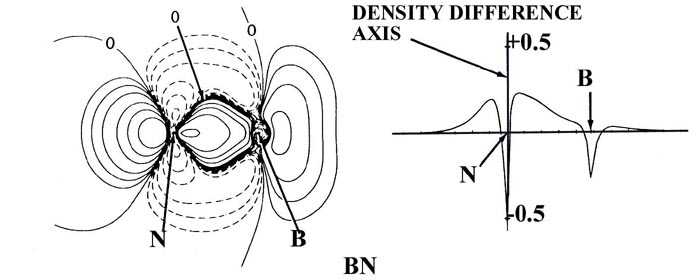
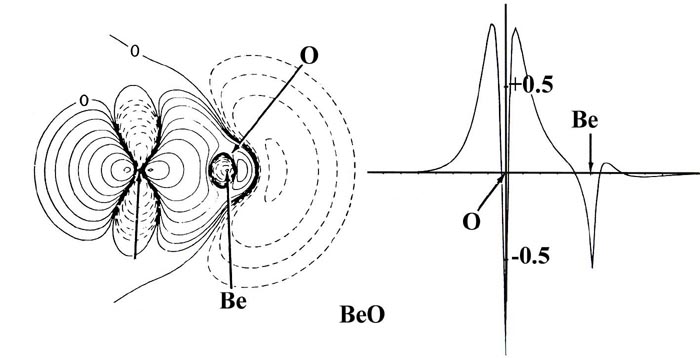
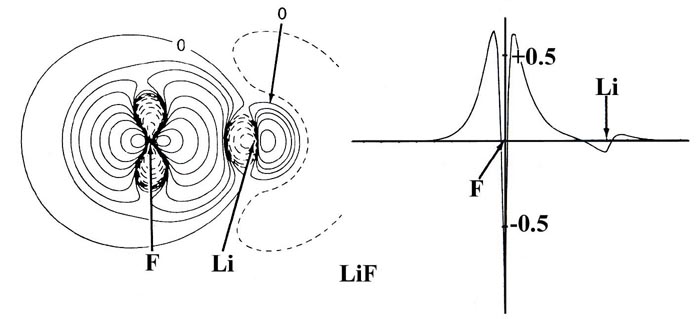
Fig. 7-10.  Bond density maps and profiles along the internuclear axes for the 12-electron sequence of molecules C₂, BN, BeO and LiF. Click here for contour values.

The charge distribution of BN  (with nuclear charges of five for boron and seven for nitrogen) is similar to that for C₂ in that charge is accumulated in the nonbonded regions of both nuclei as well as in the region between the nuclei. However, the buildup of charge behind the boron nucleus is smaller than that behind the nitrogen nucleus and the charge density shared between the nuclei is heavily shifted towards the nitrogen nucleus. Thus the binding in BN is predominantly covalent, but the bond density is polarized towards the nitrogen.

   The charge transfer in BeO and LiF is much more extreme and the bond density maps show a considerable loss of charge from the nonbonded regions of both the Be and Li nuclei. Notice that except for contours of very low value the charge density in BeO, as in LiF, is localized in nearly spherical distributions on the nuclei, distributions which are characteristic of Be⁺² and O^-2 ions. A count of the number of electronic charges contamed within the spherical or nearly spherical contours centred on the nuclei in BeO and LiF indicates that the charge distributions correspond to the formulae Be^+1.5O^-1.5 and Li⁺¹F^-1. That is, the binding is ionic and corresponds to the transfer of approximately one charge from Li to F and of one and one half charges from Be to O. Thus while the binding in LiF is close to the simple orbital model of Li⁺(1s²)F^-(1s²2s²2p⁶) as noted before, the binding in BeO falls somewhat short of the description Be⁺²(1s²)O^-2(1s²2s²2p⁶). Notice that the density contours on oxygen in BeO are more distorted towards the Be than the contours on F are towards Li in LiF. This illustrates that the oxygen anion is more polarizable than is the fluoride anion.

   The radius of the charge distribution on the nonbonded side of the Be nucleus as measured along the bond axis is identical to that found for an isolated Be⁺² ion. (Recall that the radius of an atomic or orbital density decreases as the nuclear charge increases. Thus the Li⁺¹ ion is larger than  the Be⁺² ion as indicated in Fig. 7-9.) However, the radius of the Be charge density perpendicular to the bond axis is much greater than that for a  Be⁺² ion. This shows, as does the actual electron count given above, that the two valence electrons of boron are not completely transferred to oxygen in the formation of the BeO molecule.

    Hydrogen is an exception to the above set of generalizations regarding an element's position in the periodic table and the ionic-covalent nature of the bond it forms with other elements. It does not behave in a manner typical of family IA. The bond formed between hydrogen and another member of group IA, as exemplified by LiH, is ionic and not covalent. Here hydrogen accepts a single electron to fill the vacancy in its 1s shell and thus resembles the members of family VIIA, the halogens. The bond in HF, however, is more polar than would be expected for the union of two adjacent  members of the same family, and hydrogen is therefore not a typical  member of family VIIA. This intermediate behaviour for H is understandable in that the values of its ionization potential and electron affinity are considerably greater than those observed for the alkali metals (IA) but are considerably less than those found for the halogens (VIIA).