An Introduction to the Electronic Structure of Atoms and Molecules

Dr. Richard F.W. Bader 
Professor of Chemistry / McMaster University / Hamilton, Ontario


Preface
1.  The Nature of the Problem
2.  The New Physics
3. The Hydrogen Atom
  • Introduction
  • The Quantization of Energy
  • The Probability Distribution of the Hydrogen Atom
  • Angular Momentum of an Electron in an H Atom
  • Some Useful Expressions
  •  Problems
4.  Many-Electron Atoms
5.  Electronic Basis for the Properties of the Elements
6.  The Chemical Bond
7.  Ionic and Covalent Binding
8.  Molecular Orbitals
Table of Contour Values
 

The Hydrogen Atom

The study of the hydrogen atom is more complicated than our previous example of an electron confined to move on a line. Not only does the motion of the electron occur in three dimensions but there is also a force acting on the electron. This force, the electrostatic force of attraction, is responsible for holding the atom together. The magnitude of this force is given by the product of the nuclear and electronic charges divided by the square of the distance between them. In the previous example of an electron confined to move on a line, the total energy was entirely kinetic in origin since there were no forces acting on the electron. In the hydrogen atom however, the energy of the electron, because of the force exerted on it by the nucleus, will consist of a potential energy (one which depends on the position of the electron relative to the nucleus) as well as a kinetic energy. The potential energy arising from the force of attraction between the nucleus and the electron is:
 
Let us imagine for the moment that the proton and the electron behave classically. Then, if the nucleus is held fixed at the origin and the electron allowed to move relative to it, the potential energy would vary in the manner indicated in Fig. 3-1. The potential energy is independent of the direction in space and depends only on the distance r between the electron and the nucleus. Thus Fig. 3-1 refers to any line directed from the nucleus to the electron. The r-axis in the figure may be taken literally as a line through the nucleus. Whether the electron moves to the right or to the left the potential energy varies in the same manner.


Fig. 3-1. The potential energy of interaction between a nucleus (at the origin) and an electron as a function of the distance r between them.

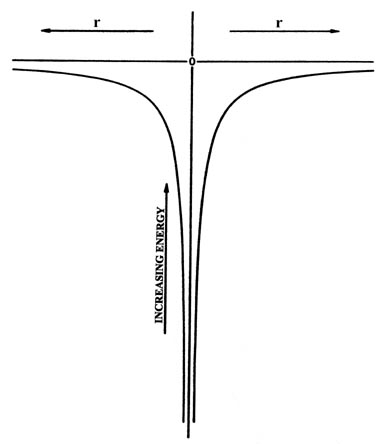
The potential energy is zero when the two particles are very far apart (r = ¥ ), and equals minus infinity when r equals zero. We shall take the energy for r = ¥ as our zero of energy. Every energy will be measured relative to this value. When a stable atom is formed, the electron is attracted to the nucleus, r is less than infinity, and the energy will be negative. A negative value for the energy implies that energy must be supplied to the system if the electron is to overcome the attractive force of the nucleus and escape from the atom. The electron has again "fallen into a potential well." However, the shape of the well is no longer a simple square one as previously considered for an electron confined to move on a line, but has the shape shown in Fig. 3-1. This shape is a consequence of there being a force acting on the electron and hence a potential energy contribution which depends on the distance between the two particles. This is the nature of the problem. Now let us see what quantum mechanics predicts for the motion of the electron in such a situation.