An Introduction to the Electronic Structure of Atoms and Molecules

The potential field of a nucleus in an atom is spherically symmetric, depending only on the distance between the nucleus and the electron. Consequently the spatial symmetries of atomic orbitals are completely determined by the angular momentum quantum numbers l and m. When spherical polar coordinates rather than cartesian coordinates are used to describe the orbitals (Fig. 8-3) the dependence of the orbitals on the angles q and f is determined by their angular momentum quantum numbers.

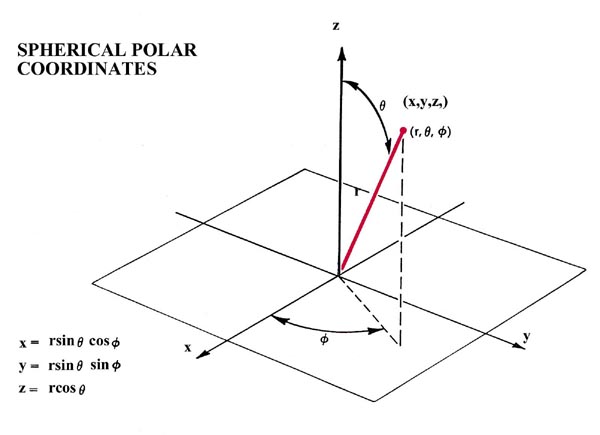
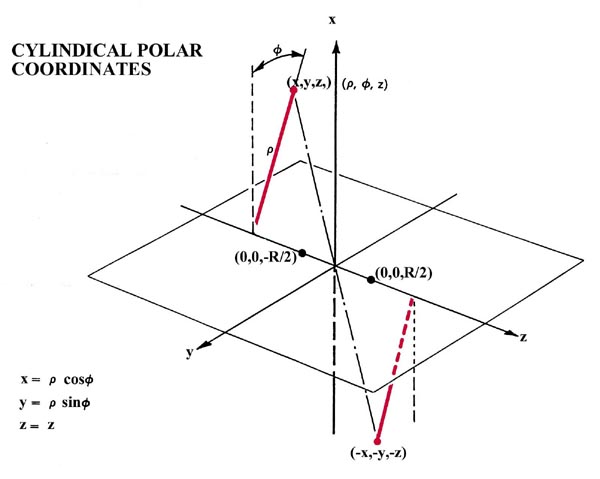
Fig. 8-3.  The relationships of spherical polar and cylindrical polar coordinate systems to the Cartesian axes x, y and z. The inversion operation transforms the point (x,y,z) into the point (-x,-y,-z).

Only the radial dependence (the dependence of the orbital on the coordinate r, the distance between the nucleus and the electron) differs between orbitals with the same  l and m values but different values of n.

   The potential field of the nuclei in a linear molecule possesses cylindrical symmetry. In terms of a cylindrical coordinate system (Fig. 8-3) the single angular momentum quantum number l determines the dependence of the molecular orbitals on the angle f, a dependence determining the symmetry of the orbital for a rotation about the internuclear axis. The dependence of the molecular orbitals on r and z is left undetermined.

   The forms of the orbitals are not as fully determined by the angular momentum quantum numbers in a molecule as in an atom. However, we may further characterize and label the orbitals for a molecular system by taking advantage of the symmetry possessed by the molecule. The symmetry of the potential field in which an electron moves places very severe restrictions on the possible forms of the orbitals. This is a very general and powerful result. Indeed, the angular dependence of orbitals and wave functions and their angular momentum quantum numbers may be completely determined solely by a consideration of the rotational symmetry of a system.

   We may illustrate the role which symmetry plays in determining the form of an orbital by considering the symmetry properties of the orbitals obtained in Section 2 for the case of an electron restrained to move on a line of fixed length. Let us shift the origin of the x-axis in the plots of the orbitals (Fig. 2-8) to the mid-point of the line, thereby changing the values of the coordinates of the two end points from 0 and L to -L/2 and +L/2 respectively. Next let us denote by the symbol R the operation of reflection through the origin, an operation which replaces each value of x by -x. For example, the end points x = -L/2 and x = +L/2 are interchanged by the reflection operator R.

   The first point to note about the operation of reflection is that its application leaves the phyiscal system itself unchanged. The potential in which the electron moves is assumed to be of constant value along the x-axis. The reflection operator simply interchanges the two halves of the line leaving the system unchanged. The potential is said to be invariant to the operation of reflection through the origin.

   What is the effect of R on the wave functions or orbitals? When R operates on y₁(x) (that is, when y₁(x) is reflected through the origin) the result is obviously to change y₁(x) into itself:
 

The reflected function y₁(-x) is indistinguishable from y₁(x).

   The result of operating on y₁(x) with the operator R is to leave the function unchanged. y₁(x) is said to be symmetric with respect to a reflection through the origin. The operation of R on y₂(x) yields a different result:
 

It is obvious from Fig. 2-8 that the reflection of y₂(x) through the mid-point changes its sign, the reflected function y₂(-x) is the negative of the unreflected function y₂(x). Such a function is said to be antisymmetric with respect to a reflection at the origin. Every orbital for this system is either symmetric (those with odd n values) or antisymmetric (those with even n values) with respect to the symmetry operation of reflection.

   Any orbital which was neither symmetric nor antisymmetric but was instead simply unsymmetrical with respect to reflection would when squared yield an unsymmetrical probability distribution. An unsymmetrical probability distribution implies that the electron is more likely to be found on one half of the x-axis than on the other. This is a physically unacceptable result since there are no forces acting on the electron which would favour one end of the line over the other. Only orbitals which are either symmetric or antisymmetric yield density distributions which properly reflect the symmetry of the system (Fig. 2-4), that is, density distributions which are themselves symmetrical with respect to reflection at the mid-point of the line.

   Thus we conclude that the only wave functions resulting in physically acceptable probability distributions are those which are either symmetrical or antisymmetrical with respect to any symmetry operation which changes the physical system into itself. This statement is always true for non-degenerate wave functions, but must be amended somewhat for the action of some symmetry operations on a degenerate set of wave functions.

   We shall use only one of the many symmetry elements possessed by a homonuclear diatomic molecule to further characterize and classify the molecular orbitals. A homonuclear diatomic molecule possesses a centre of symmetry and the corresponding operator is called the inversion operator. The action of this operator, denoted by the symbol i, is to replace the x, y, z coordinates of every point in space by their negatives -x, -y, -z. This corresponds to an inversion (or reflection) of every point through the origin or centre of symmetry of the molecule (Fig. 8-3).

   The action of the inversion operator on the nuclear coordinates simply interchanges one nucleus for the other. Since the nuclei possess identical charges, the nuclear framework is left unchanged and the potential exerted by the nuclei is invariant to the operation of inversion. Thus every molecular orbital for a homonuclear molecule must be either symmetric or antisymmetric with respect to the inversion operator. Orbitals which are left unchanged by the operation of inversion (are symmetric) are labelled with a subscript g, while those which undergo a change in sign (are antisymmetric) are labelled u. The symbols g and u come from the German words "gerade" and "ungerade" meaning "even" and "odd" respectively.